在Dana的文章中，参数化这个名词并没有给出准确的定义。Dana既没有将自己对晶体的描绘阐述为参数化，也没有认为自己的设计是用参数化的方式来表达的（不像Patrik Schumacher现在（2009a, 15）将参数化作为一个划时代的新风格的词语）。相反，Dana使用了参数化最原始的数学含义，把参数化作为一个和其他诸如平行、相交、平面等没有太大差别的数学术语。

参数化，在1837年Dana使用和现在数学家使用时，它表示了一种被《数学简明百科全书》解释为“表示若干独立变量的显函数的方程，被称为参数“这一定义阐述了两个关键标准：

1、 参数化的等式使用一系列参数来表达变量

2、 变量计算的结果与显函数中的参数有关。这是在之后的定义中非常重要的一点内容，因为有些当代建筑师认为相关性构成了参数化的相互关系。

数学Tips:

解析式中明显地用一个变量的代数式表示另一个变量时，称为显函数

一个参数化等式的例子，悬链线的方程：

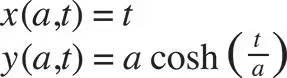
数学Tips:

悬链线(Catenary) 是一种曲线，因其与两端固定的绳子在均匀引力作用下下垂相似而得名。适当选择坐标系后，悬链线的方程是一个双曲余弦函数。

这两个等式满足参数化方程的标准。对于第一条：等式用一组参数（参数a，控制了曲线的形状；参数t，控制了曲线与轴的交点位置）来表达了一组变量（在这里是变量x和变量y）。对于第二条，等式的结果（x和y）与显函数的参数（a和t）有关。

这是术语“参数化”的起源：一组由若干参数通过显函数表达的变量。

模拟（非数字化）的参数化： 高迪

除了1837年Dana关于参数化晶体绘图的文章，19世纪还有许多科学与数学与参数化关联的例子。John Leslie（1821,390）爵士的例子便发生在那个时代，在他几何学分析的论著中，用“参数化的圆”证明了悬链线的自相似性。另一个例子是Samuel Earnshaw（1839，102）写的一篇论文，论述了“参数化双曲面”在线性力作用下的变形，从而给出了Earnshaw定理。上面的例子只是使用参数化方程表示几何体的众多例子中的两个，那时是19世纪末，在Antoni Gaudi第一次使用参数化悬链线和参数化双曲抛物面设计曲面之前。

物理Tips：

恩绍定理(Earnshaw's theorem)指出点粒子集不能被稳定维持在仅由电荷的静电相互作用构成的一个稳定静止的力学平衡结构。通俗的来讲，举一个磁场的例子，将一块磁铁飘浮在另一块磁铁之上是不可能的。

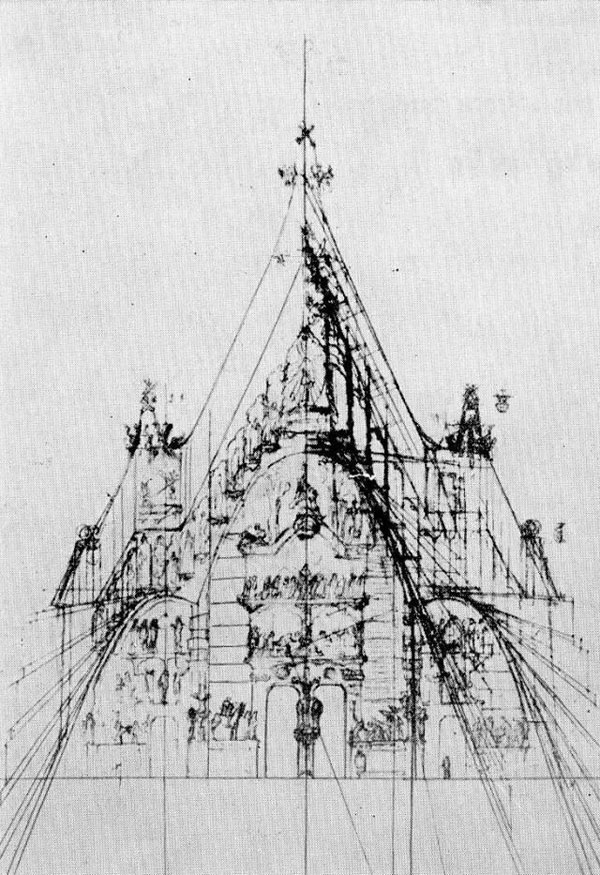
我们没法知道高迪是否受到了用参数化等式来定义几何体的科学家和数学家们的直接影响。现在圣家堂的执行建筑师Mark Burry（2007a，11）表示, 高迪自己几乎没有写下过任何关于不断超越极限的动力、理论和实践的文字。众所周知，高迪在大学上曾修读过高级数学、普通物理、自然科学和画法几何。高迪对数学的深刻认识是他建筑学的基础，特别对于他晚期的建筑来说。他晚期的建筑几乎包含了所有的数学直纹曲面——螺旋面，抛物面，双曲面，它们通过直纹线，布尔值，比率和悬链线的参数化方法联系在一起。无论高迪是否知道在他之前对于参数化定义几何体的研究工作，高迪肯定在设计建筑时，使用了以参数化方程为基础的模型。

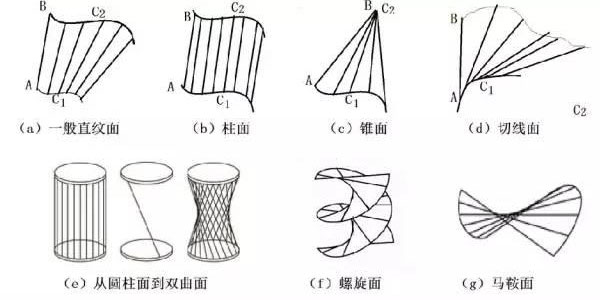
数学Tips：

如果曲面方程为r(u,v)=a(u)+v*l(u)，其中l(u)为单位向量，则称此曲面为直纹面(ruledsurface)

这时v曲线为直线，因此直纹面是由一条条直线所织成，这些直线就称为此直纹面的（直）母线。柱面和锥面都是直纹面。二次曲面中的单叶双曲面和双曲抛物面（马鞍面）也是直纹面。

Hooke（1675,31）关于悬链模型的字谜，在那时，这样的形式经常被用作结果发布前首次声称一个观点的方法。

在高迪的建筑中，我们可以经常看到其使用参数化方程的线索，但也许最能说明这一点的是他对悬链模型的使用。悬链模型起源于1675年Robert Hooke的字谜“abcccddeeeeefggiiiiiiiiillmmmmnnnnooprrsssttttttuuuuuuuuu”，它转译自拉丁语“悬挂的自由曲线，反转过来可以成为精确的拱形。”高迪使用这一定理来设计古埃尔公园礼拜堂。他通过将铅弹寄在绳子下来获得礼拜堂倒立的模型。根据Hooke的定律，悬索会形成一种形态，当倒置时，所有的部分都只会收到压力。悬链模型具有参数化方程的所有要素。它具有一系列的独立参数（绳长，锚点位置，铅弹等重量），并且它有一系列的输出结果（绳上不同点的不同位置），它由参数通过显函数生成（在这里是牛顿运动学定律）。通过改变这个参数化模型中的独立参数，高迪可以生成各种版本的古埃尔公园里礼拜堂方案，并且可以确信其结构一定是纯受压的。

古埃尔公园中悬挂的高迪的悬挂模型