与早期科学家和数学家使用的参数化方程相比，高迪的悬挂模型的创新关键是，它能够自动的计算出其参数化方程的结果。高迪可以通过重力对绳索的作用，轻易地获得悬链线的形状，而不是手工的计算悬链线的参数方程。这种模拟计算方法被Frei Otto所发展，例如源自肥皂薄膜的极小曲面和通过浸在液体中的羊毛生成的最小路径。

Otto（1996）使用了这些找形模型进行了设计。一种通过探究自然的参数化建模方式。在高迪的项目中，悬链模型在方便其找形的同时也使他的设计具有结构合理的形体，而且当高迪调整模型的参数时，模型的形态也会自动的发生改变。这组成了参数化建模教义非常重要的一部分，即参数化建模的优点建立在探索的结果的基础上。最初对于参数化的定义并没有改变，这些通过模拟化实现的参数化模型，都具有一系列的通过独立的参数与显函数运算而得到的量。然而这都建立在对模型提供的可能性的探索之上。

曼海姆多功能大厅屋顶, 1970-1975年, 德国曼海姆 ，Frei Otto

联邦园艺博览会音乐馆, 1955年, 德国 卡塞尔，Frei Otto

Frei Otto Tips：

Frei Otto 定义了三种不同的基本形式：

1. Direct path networks,

2. Minimal path networks,

3. Minimizing detour networks。

1. Direct path networks, 即连接所有目的地的点，获得最直接，也最不费脑子的路径。下图是Rhino中五个点全部连接的一个 Direct path networks.

直接路径图例

2、对于Minimal path networks的研究，FreiOtto再次使出了杀手锏，即利用物质本身属性，来研究模拟自然条件下所存在的最节约能量的稳态。这次他使用的道具是肥皂。

下图是肥皂泡模拟的Minimalpath system，所谓的最短路径，就是优化之后的所有线段的长度最短。图中有比较，原来三点之间的Direct path长度为2，但是利用肥皂泡原理得到的120°夹角路径，长度为1.93，实现了路径长度的优化。minimal path system, 顾名思义，通过这个严格的数学方式得到的最终结果，路径总长是唯一的一个定值，也就是理论上的最小值，这个模型最终是一个树状模型，没有任何冗余的连接。

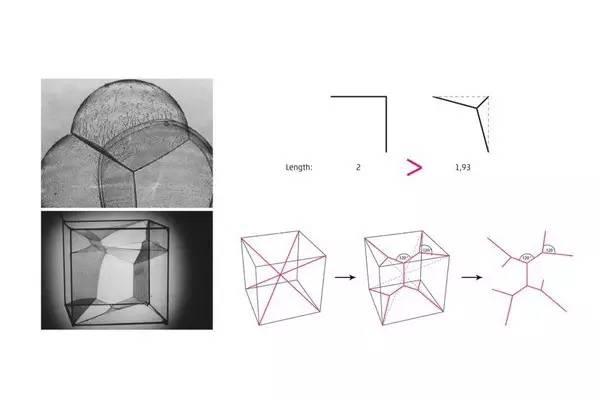
最短路径图例

3、第三个基本形式Detour path networks中出现了FreiOtto另一个非常有名的模拟实验，是的，他又用道具了，这次用到的是羊毛线模型 Wool-thread model. 左图为连接各个目的点的干燥的羊毛，右图为湿润的羊毛。湿润的羊毛彼此之间因为水的张力作用吸附在了一起，形成了多个路径变为一个路径的转变。这个实验的意图在于减少各个目的点的Direct path的总长度，同时让绕圈因素维持在一个比较低的范围。3.Detour path networks 和 2. Minimal path networks 有很多相似点，都是为了缩短路径，不同处在于，后者2更倾向于用一个完美的数学思路来模拟，得到的是唯一解。而前者3得到的模拟结果并不是唯一的，因为诸多影响因素的不同，而最终会得到不同的结果，但是这些结果的共同目标都是优化路径总长度。

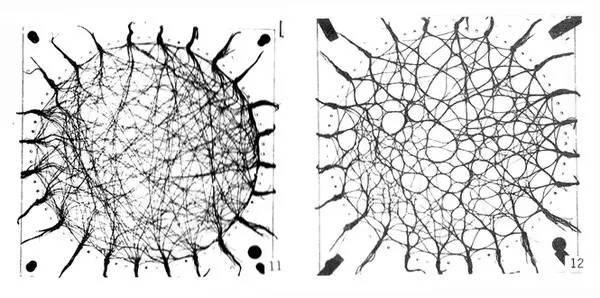
羊毛物理方法示意

对于Detour path system的利用也是非常广泛，因为在建筑行业中，设计并不是唯一解，比如说做城市设计，绝对不会有要求说这片地最后的道路总长一定要满足Minimal path的理论最小值。相反，一个有多个可控参数，可调整又可优化路网总长度的模拟工具不是更好？Detour path system 横空出世，来看Zahahadid事务所2006年在伊斯坦布尔做的这个城市设计，下面的视频摘自其官网，模拟了如何从Directpath到优化后的道路（下图的形状）的渐变过程，形象生动。

Zaha Hadid 使用Detour path system进行伊斯坦布尔城市设计

文章翻译并编辑自Daniel Davis 《A History of Parametric》

胡雨辰 同济大学建筑与城市规划学院硕士研究生